１、水平な三気筒機



120°単式三気筒機についての図。左側を基準とし、右先行を例とした。クランクが120°割りになってるので、60°ごとに何れかの気筒が死点にあるのは理解しやすい。

･･･がしかし、主動輪が第２動輪だとメインロッドが第１動輪の軸と重なって困るから回避しなければならない。よっぽど車両限界に余裕があって、要求出力もほどほどなんだったら第１動輪を主動輪とすれば回避もできるんだが･･･


２、中央気筒を持ち上げて回避する。

そこで中央気筒を持ち上げて避けてみる。



ψ°だけ持ち上げて回避したとき、そのままでは動作タイミングがずれる。そこで、クランク軸もψ°だけ遅らせる。すると･･･


中央気筒が前死点にあるときは･･･


ということで、元と同じく左が60°進んだときに前死点に至る。後死点は



という具合で、きちんと左が240°のときに来る。ということで単式３気筒機の動作は、クランクやメインロッドから見ると殆ど問題になるような点は無い。

唯一、中央ピストンの水平分力がcosψ倍され、またsinψ倍された力が垂直に働くことになるのが問題と言えば問題だが、ψの値がそれほど大きくなければ誤差みたいなものなので気にする必要は無い。

３、ディバイデッドドライブ

他の回避方法としては、中央気筒をかける軸を変えてしまう方法がある。



これなら持上げる必要は無くなるが、先台車とのクリアランスを取れるかどうかという問題が出てくる。

モノを往復運動させるにゃ力が必要なり。回転させれば遠心力が働く。クランク振り回すのはハンマー投げと同じこと。そして振動が発生する。普通は振動が発生して良いことなんかひとつも無いので、これをどうにか釣り合わせようとする。そんな話の蒸気機関車版。


１、考え方の把握

足回りの、運動しててアンバランスそうな部分に注目する。各部名称はよろしいでせう。



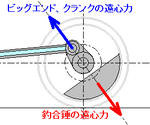
回転部に注目する。ビッグエンド、クランクと、軸をはさんで反対側についてる錘。これは完全にバランスしてて、遠心力どうしは打ち消しあっている。これがバランシングの基本となる。








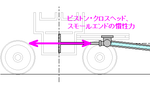
次にピストン・クロスヘッド・スモールエンドに注目すると、これは往復運動するばっかりなので慣性力がレール方向に生じる。これはほっとけばそのまま振動のネタになるので、バランシングを施す。

慣性力は、はじっこで最大になる。




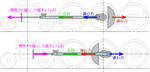
はじっこになったときをの全体を見て、働いてる力の合計を見る。

すると、合計の力と反対向きに錘の遠心力が働いてるので、その分錘を重くすることで、慣性力を100％打ち消してみる。つまり、クランクの遠心力の分から超過させる。



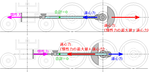
見合うだけ増やしたら、水平はゼロになった。水平方向の振動は無くなった。だがしかし･･･





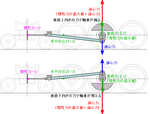
クランクが縦になったときを見てみると、超過ぶんは相手が無いのでそのまま縦方向の力となって軸重を変動させてしまう。これがハンマーブロウである。ようするに、バランシングとは錘を使って往復慣性力が働く方向を90度変えることなんである。



だがしかし、このハンマーブロウは線路を破壊したり、スリップの元になったりと悪いことばかり。さりとて往復部は釣り合わせたい。だから蒸気機関車では、一般的には妥協して33～50％だけ釣り合わせることになる。国鉄では25％しか釣り合わせなかったためレール方向の振動が激しかったんである。

２、計算する
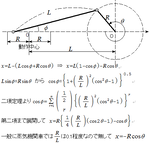
簡単にするため･･･というよりは蒸気機関では一般的な手法として、変位x＝－クランク半径R×cos（クランクの進角θ）を用いる。









ここで角運動量ωを確認。１秒間にどんだけの角度を回転するかのことなのだけれど、2π[rad]＝360[°]、回転円の周上での速度をV[m/秒]、回転半径r[m]として、回転数n[回転/分]のとき、運動した距離は円周[m]×回転数n[回転/分]＝2×π×r×n[m/分]＝2×π×r×n[m/60秒]＝2×π×r×n÷60[m/秒]より、

　　角運動量ω[rad/s]＝速度V[m/秒]÷回転半径R[m]
　　角運動量ω[rad/s]＝２×円周率π×回転数n[回転/分]÷60[秒]

また遠心力は回転してる錘の質量をm[kg]として、

　　遠心力f[kg]＝質量m[kg]×回転半径r[m]×角運動量ω[rad/秒]^2
　　遠心力f[N]＝質量m[kg]×回転半径r[m]×角運動量ω[rad/秒]^2÷重力加速度g[m/秒^2]

さて、超過釣合錘の遠心力の作用点はクランクの中心なので、そこから遠心力の矢印を書いて、これを水平と垂直に分解して慣性力と一緒に図示してみる。
慣性力の作用点はクランク軸だけど見にくくなるからごまかすよ(´･ω･)ノ



後ろ死点を起点としてクランクの進角を取ると、右を正とし、

　　ピストンの変位x[m]＝クランク半径R[m]×cosθ
微分して
　　ピストンの速度v[m/秒]＝－R×ω×sinθ
微分して
　　往復部の加速度α[m/秒^2]＝－R×ω^2×cosθ
往復部の質量M[kg]として加速に逆らう力である慣性力F=－α×Mより
　　慣性力F＝M×R×ω^2×cosθ

遠心力は錘の質量をm[kg]、錘の重心の回転半径をr[m]として、
　　遠心力f[kg]＝m×r×ω^2
またクランクの進角θ[rad]として
　　水平分力fh[kg]＝m×r×ω^2×cos(θ+π)＝－m×r×ω^2×cosθ
　　垂直分力fv[kg]＝m×r×ω^2×sin(θ+π)＝－m×r×ω^2×sinθ
垂直分力はそのままハンマーブロウとなる。

慣性力と水平分力を合計すると、
　　M×R×ω^2×cosθ－m×r×ω^2×cosθ＝(M×R－m×r）×ω^2×cosθ

３、まとめ

ということで、超過釣合錘m[kg]の重心の回転半径r[m]、往復部の質量M[kg]、クランク回転半径R[m]、動輪回転数n[回転/分]のとき、

　ハンマーブロウfv[kg]＝－m×r×(2×π×n÷60)^2×sinθ
　不釣合力Fub[kg]＝(M×R－m×r）×(2×π×n÷60)^2×cosθ
　釣合率ξ[％]＝m×r÷(M×R)×100

内燃機関のようにロッドが短い機関を考えるときは、往復部について2θの項まで考えておけば充分である。